A state consisting of
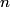 identical bosons labeled identical bosons labeled 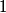 , , 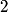 , ..., , ..., 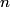 must satisfy must satisfy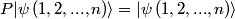 where 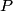 is an operator that permutes the is an operator that permutes the 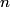 particles. This defines a symmetric state. particles. This defines a symmetric state.A state consisting of 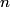 identical fermions labeled identical fermions labeled 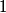 , , 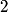 , ..., , ..., 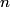 must satisfy must satisfy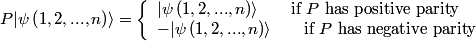 where 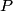 is again an operator that permutes the is again an operator that permutes the 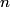 particles. This defines an antisymmetric state. particles. This defines an antisymmetric state. It is only possible to antisymmetrize a collection of single-particle states when all of the single-particle states are distinct -- this is the statement of the Pauli exclusion principle. The Pauli exclusion principle applies only to multi-fermion states i.e. it is possible to symmetrize a collection of single-particle states regardless of whether there is redundancy. Collecting all of this information, \begin{itemize} \item Bosons have symmetric wavefunctions. \item Fermions have antisymmetric wavefunctions. \item Bosons do not obey the Pauli exclusion principle. \item Fermions do obey the Pauli exclusion. \end{itemize} Therefore, answer (D) is correct. |